|
It is an unsolved problem, whether there is a convex table in the plane
such that the exterior billiard dynamical systems has an unbounded orbit.
The problem had been suggested in 1960 by B.H. Neumann.
It appeared listed as an unsolved problem in Mosers book "stable and
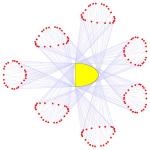
unstable motion". Serge Tabatchnikov suggested to look at the semi circle.
Numerical experiments show there, that an orbit escapes to infinity. But
this is not proven. Here are some numerically computed orbits. Update since posting this page in the year 2005: there are polygons known now for which the map is unbounded: see Outer billiards on kites by Richard Evan Schwartz. Update 2009: there is now a book on the proof. Here is the first page of that book, which contains some milestones on the Moser-Neumann problem: 
Source: Outer Billiards on Kites (AM-171)
by Richard Evan Schwartz, 2009.
|
