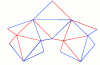
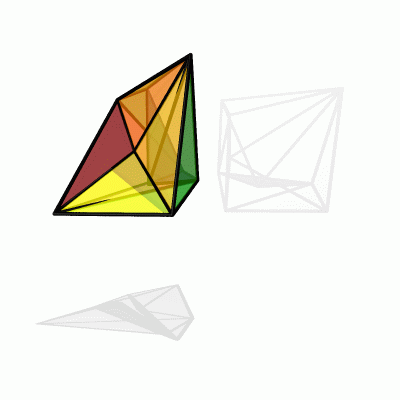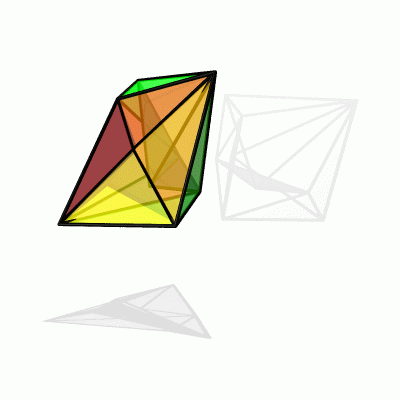
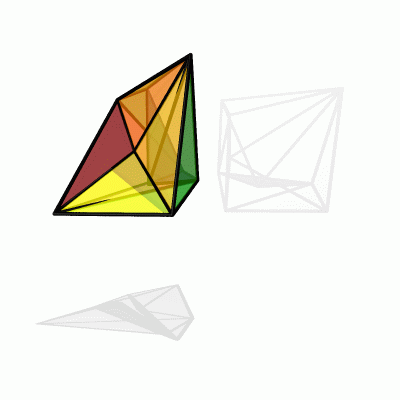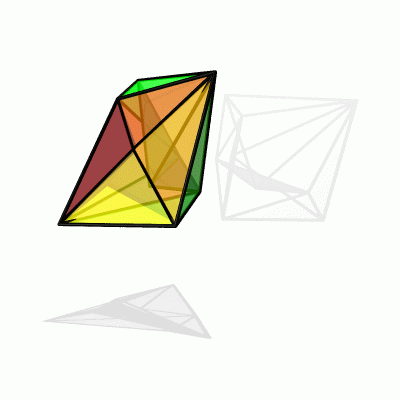
While a theorem of Cauchy excludes continuous deformations of
convex polyhedra, this is possible for
nonconvex surfaces as shown first by Connelly in 1977.
The example here is due to Klaus Steffen. Challenge: can one give
explicit formulas for the motion of the points during the
deformation?
The Povray 3.1
program which computed the surface in this page determined
the points by solving a system of quadratic equations for the 27 unknowns.
This happened by folding up the surface using two free
parameters (see the unfolded paper model).
In some sense, the geometry defines already the Groebner
basis to solve the nonlinear system of equations. One parameter necessary
to fit the triangles together was then determined numerically.
|
While a theorem of Cauchy excludes continuous deformations of
convex polyhedra, this is possible for
nonconvex surfaces as shown first by Connelly in 1977.
The example here is due to Klaus Steffen. Challenge: can one give
explicit formulas for the motion of the points during the
deformation?
The Povray 3.1
program which computed the surface in this page determined
the points by solving a system of quadratic equations for the 27 unknowns.
This happened by folding up the surface using two free
parameters (see the unfolded paper model).
In some sense, the geometry defines already the Groebner
basis to solve the nonlinear system of equations. One parameter necessary
to fit the triangles together was then determined numerically.
