![[Geometric Setup]](graph1.gif)
The planimeter is a mechanical device for
measuring areas in the plane. It has the shape of a ruler with two legs.
One leg of length 1 connects the fixed origin (0,0) to (a,b).
A second leg of length 1 connects (a,b) with the end point (x,y).
The point (x,y) determines (a,b) as the intersection
of two unit circles centered at (0,0) and (x,y). The intersection
is unique if the angle between the two planimeter legs is smaller than 180
degrees. The measurement consists of dragging (x,y) along the boundary of the region R. The wheel at (x,y) measures the motion in the direction orthogonal to the leg. After completing the path along the boundary of the region R. the total wheel rotation indicates the area of the region. Why?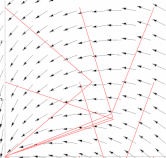 
Let F(x,y)=(P(x,y),Q(x,y)) be the Planimeter vector field. It is
defined by attaching a unit vector orthogonal to the vector (x-a,y-b) at (x,y).
The weel rotation is the line integral of F along the boundary of R.
Green's theorem tells that this integral is the double integral of
curl(F) over the region R. The planimeter vector field is explicitely
given by F(x,y)=(P(x,y),Q(x,y))=(-(y-b(x,y)),(x-a(x,y))).
Furthermore, curl(F)=Qx-Py
is equal to 2+(-ax-by) which is 2 plus
the curl of the vector field G(x,y)=(b(x,y),-a(x,y)). A direct
verification shows that curl(G)=-1.
The Planimeter lineintegral is therefore the area of the
enclosed region.
|
